一、等比中项的表达式

若数a，G，b成等比数列，那么就称G为a与b的等比中项，从而有G2＝ab或G＝± 。
二、等比中项的理解：
1.如果a，G，b三个数成等比数列，则有G2=ab．反之不一定成立．由等比中项定义可知： ，  ，
2.这表明，只有同号的两项才有等比中项，并且这两项有2个互为相反数的等比中项，当a>0，b>0时，G 又叫做a，b的几何平均数。

 
三、等比数列的有关概念
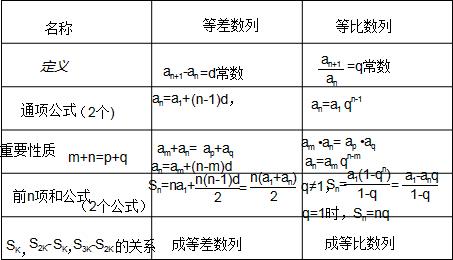
(1)定义：
如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数(不为零)，那么这个数列就叫做等比数列.这个常数叫做等比数列的公比，通常用字母q表示，定义的表达式为an+1/an=q(n∈N*，q为非零常数).
(2)等比中项：
如果a、G、b成等比数列，那么G叫做a与b的等比中项.即：G是a与b的等比中项a，G，b成等比数列G2=ab.
四、等比数列的有关公式
(1)通项公式：an=a1qn-1.
五、等比数列{an}的`常用性质
(1)在等比数列{an}中，若m+n=p+q=2r(m，n，p，q，r∈N*)，则am·an=ap·aq=a.
特别地，a1an=a2an-1=a3an-2=….
(2)在公比为q的等比数列{an}中，数列am，am+k，am+2k，am+3k，…仍是等比数列，公比为qk;数列Sm，S2m-Sm，S3m-S2m，…仍是等比数列(此时q≠-1);an=amqn-m.
六、等比数列的特征
(1)从等比数列的定义看，等比数列的任意项都是非零的，公比q也是非零常数.
(2)由an+1=qan，q≠0并不能立即断言{an}为等比数列，还要验证a1≠0.
七、等比数列的前n项和Sn
(1)等比数列的前n项和Sn是用错位相减法求得的，注意这种思想方法在数列求和中的运用.
(2)在运用等比数列的前n项和公式时，必须注意对q=1与q≠1分类讨论，防止因忽略q=1这一特殊情形导致解题失误.