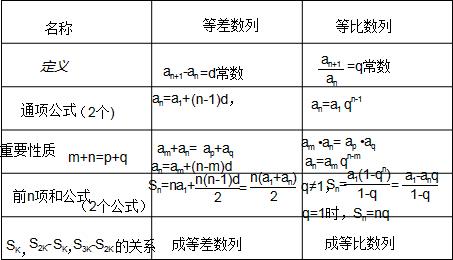
等比数列的定义和性质-等差数列和等比数列的区别和联系详细信息
| 宜城教育365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载网免费提供课件、试题、教案、学案、教学反思设计等备课365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载。数百万365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载,无须注册,天天更新! |
|
|
|
|

数学365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载
数学试题列表
|
数学中高考列表 |
||||

免责声明 :本站365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载版权归原着作人所有,如果我们转载的作品侵犯了您的权利,请通知我们,我们会及时删除。
宜城教育365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载网主办 站长:此地宜城 邮箱:yrqsxp@163.com QQ:290085779