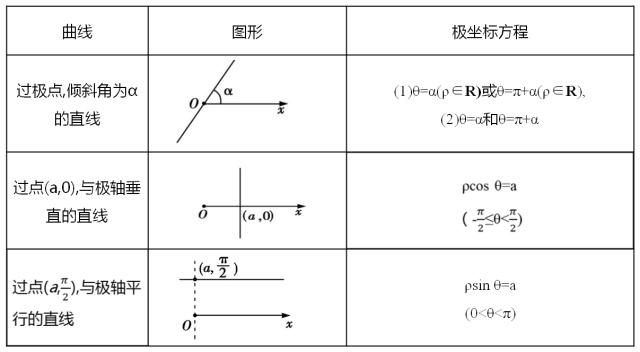
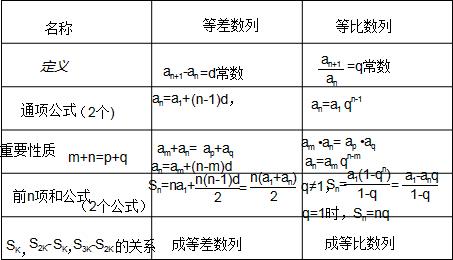
| 宜城教育365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载网www.bjtlcd.com 一、共轭复数的性质
1.当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数。
2.虚部不等于0的两个共轭复数也叫做共轭虚数。
3.复数z=a+bi和 =a-bi(a、b∈R)互为共轭复数。

二、复数加减法的几何意义运算法则
1、复数z1与z2的和的定义:z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i;
2、复数z1与z2的差的定义:z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i;
3、复数的乘法运算规则:设z1=a+bi,z2=c+di(a、b、c、d∈R)是任意两个复数,那么它们的积(a+bi)(c+di)=(ac-bd)+(bc+ad)i,其实就是把两个复数相乘,类似两个多项式相乘,在所得的结果中把i2换成-1,并且把实部与虚部分别合并,两个复数的积仍然是一个复数。
4、复数的除法运算规则: 。
三、复数加法的几何意义:
设:OZ1,OZ2分别与复数a+bi,c+di对应,且OZ1,OZ2不共线 (如下图),以OZ1,OZ2 为邻边画平行四边形OZ1ZZ2,则其对角线OZ所表示的向量OZ就是复数(a+c)+(b+d)i对应的向量。
复数
法的几何意义:
复数
法是加法的逆运算,设:OZ1,OZ2分别与复数a+bi,c+di对应,且OZ1,OZ2不共线(如下图),,则这两个复数的差z1-z2与向量OZ1-OZ2(等于Z2Z1)对应,这就是复数
法的几何意义。
四、复数的运算律:
1、复数的加法运算满足交换律:z1+z2=z2+z1;
结合律:(z1+z2)+z3=z1+(z2+z3);
2、
法同加法一样满足交换律、结合律。
3、乘法运算律:(1)z1(z2z3)=(z1z2)z3;(2)z1(z2+z3)=z1z2+z1z3;(3)z1(z2+z3)=z1z2+z1z3
三、共轭复数:当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数。
虚部不等于0的两个共轭复数也叫做共轭虚数。
复数z=a+bi和 =a-bi(a、b∈R)互为共轭复数。
共轭复数的性质:
五、复数运算公式
(1)加法运算:设z1=a+bi,z2=c+di是任意两个复数,它的实部是原来两个复数实部的和,它的虚部是原来两个虚部的和:(a+bi)±(c+di)=(a±c)+(b±d)i。
(2)乘法运算:设z1=a+bi,z2=c+di是任意两个复数,则:(a+bi)(c+di)=(ac-bd)+(bc+ad)i。
其实就是把两个复数相乘,类似两个多项式相乘,结果中i2=-1,把实部与虚部分别合并。两个复数的积仍然是一个复数。
(3)除法运算:复数除法定义:满足(c+di)(x+yi)=(a+bi)的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商。
六、复数的性质
1.共轭复数所对应的点关于实轴对称。
2.两个复数:x+yi与x-yi称为共轭复数,它们的实部相等,虚部互为相反数。
3.在复平面上,表示两个共轭复数的点关于X轴对称。
七、复数的运算律
加法交换律:z1+z2=z2+z1
乘法交换律:z1×z2=z2×z1
加法结合律:(z1+z2)+z3=z1+(z2+z3)
乘法结合律:(z1×z2)×z3=z1×(z2×z3)
分配律:z1×(z2+z3)=z1×z2+z1×z3 宜城教育365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载网www.bjtlcd.com |