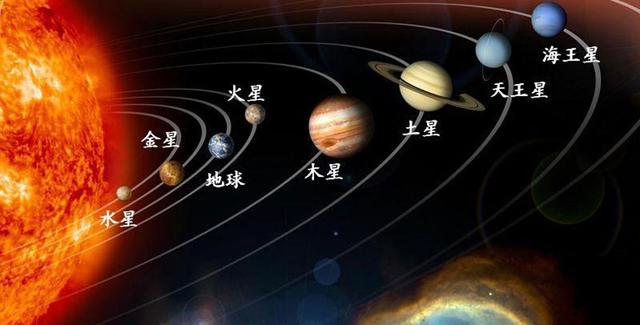
自我评价。及时反馈
【变式训练】
1、质量为8.9克的铜块挂在弹簧秤上,当铜块浸没在某种液体中时,弹簧秤的示数为7.94×10-2牛顿。求这种液体的密度。
1、该液体的密度为0.8×103千克/米3。【分析】:该题若采用常规解法逐步求解,思路不易理清,又容易出错。采用上述步骤解题要省事得多。
解:A.先对研究对象进行受力分析。该题的研究对象是浸没在某液体中的铜块,受到的力有竖直向下的重力G,竖直向上的浮力F浮和弹簧秤对它竖直上的拉力T。
B.根据力的平衡条件列方程。题目中的铜块在F浮,T和G三个力的作用下静止在液体中,所以可列出方程:T+F浮=G。

从上例的解题过程可以看出,这类题中的待求量不管是密度,还是体积,都不可能直接利用公式求解。因此都要暂时避开不予考虑,这时利用上述三个固定的步骤去解,以不变应万变。几年来,把此解题方法教给学生,并让他们找这方面的习题当堂验证,结果每题均可在教师毫无准备的情况下逐步套解,学生无不信服并乐意接受,教学效果极佳。
【变式训练】
2、如图所示,在烧杯中漂浮着一块冰,当冰完全融化为水时,水面将如何变化?

图12-30
2、冰融化后水面高度不变。【解析】:设冰融化前排开的水的体积为V1,冰融化成水的体积为V2,显然,通过比较V2与V1之间的关系,即可得知水面的变化情况:若V2=V1,水面不变;V2>V1,水面上升;V2<V1,水面下降.冰融化前根据F浮=G得:ρ水gV1=G,V1= .融化成水后质量不变,化成水的质量m水= .融化成水后质量不变,化成水的质量m水= ,化成水的体积V2= ,化成水的体积V2= = = .比较V1和V2的表达式知V1=V2,所以冰融化后水面高度不变. .比较V1和V2的表达式知V1=V2,所以冰融化后水面高度不变.
方法指导:容器中原有水的体积是一定的,液面变化是先后排开水的体积不同及冰融化成一部分水造成的.分析时要先找出引起液面变化的那部分体积(V排),根据物体的浮沉条件(力的关系)分别列式导出这部分体积的表达式,再设法比较此体积的大小,就可确定液面的变化.
3、一块冰内含有一小石块,放入盛有水的量筒内,正好悬浮于水中,此时量筒内的水面升高了4.6cm.当冰熔化后,水面又下降了0.44cm.设量筒内横截面积为50cm2,求石块的密度是多少?( 水=0.9×103kg/m3) 水=0.9×103kg/m3)
3、石块密度为3.2g/ 。【解析】从受力分析入手,并且知道冰熔化,质量不变,体积减小,造成液面下降. 。【解析】从受力分析入手,并且知道冰熔化,质量不变,体积减小,造成液面下降.
已知:S=50cm2,h1=4.6cm,h2=0.44cm
求: 石 石
V冰+V石=Sh1=50cm2×4.6cm=230 cm3冰熔化后,水面下降h2.
V′=h2S=0.44cm×50cm2=22 cm3
∵ m冰=m水
 冰V冰= 冰V冰= 水V水 水V水
 = = = = ,V水= ,V水= V冰 V冰
V′=V冰-V水=V冰- V冰= V冰= V冰 V冰
0.1V冰=22 cm3
V石=230 cm3—220 cm3=10 cm3
冰、石悬浮于水中:
F浮=G冰+G石
 水g(V冰+V石)= 水g(V冰+V石)= 水g V冰+ 水g V冰+ 水g V石 水g V石
 石= 石=
=
=3.2g/
4、在一个不大的池塘中浮着一只装满石块的小船,假如船上的人把石块投进水里,水面的高度会不会发生变化?
4、液面降低。【解析】上面的这个问题,据说是在一次国际学术会议期间,有人向三位着名的物理学家——美国的盖莫夫(1904~1968)、奥本海默(1904~1967)和布洛赫(1905~1983)提出来的,出乎意料的是,他们三人的回答没有一个是正确的。
从表面看,问题比较复杂,石块投入水中,将占据原来被水占据的空间,使池塘水面上升;同时,船的载重减小,向上浮起一些,又使池塘水面下降。既上升,又下降,综合起来究竟如何呢?
根据阿基米德原理:F浮=ρ液V排g,若要比较液面高度变化实际上只需比较出V排的前后变化情况就行了,而比较V排又可以进一步转化比较浮力的前后变化情况。
解:原来小船漂浮,对船有
F浮=G船+G人+G石
扔下石块后对船仍是漂浮的,对船有
F浮′=G船+G人 ①
石块沉底
F浮石<G石②
由①+②可得:
F浮′+F浮石<G船+G人+G石
即:F浮′+F浮石<F浮
所以它们受到的总的浮力减小。
由F浮=ρ液V排g的变形V排= 可知,ρ液不变,F浮减小(关键是比较总V排的变化)V排减小,液面降低 可知,ρ液不变,F浮减小(关键是比较总V排的变化)V排减小,液面降低
【变式训练】
1. 在探究“浸没在液体中的物体所受浮力的大小跟哪些因素有关”的实验时,部分同学提出如下猜想:
物体所受浮力的大小可能跟物体密度有关。
物体所受浮力大小可能跟物体形状有关。
……
(1)除此之外你还有什么猜想?写出你的猜想。
(2)请你就上述任一猜想,设计出实验探究方案(所选方案可以是同学提出的或自己提出的)。
考察目的与解题思路:此题的开放包括“问题开放”、“器材开放”和“过程开放”,以它的多端性和变通性考察学生的发散能力,得到对事物的全面认识。解题时,首先搞清探究目的,从多个角度大胆想象,从不同层面分析问题,利用实验室器材或生活中的日常用品有机组合,找到最简捷、最直观的实验方案。
【解析】(1)猜想有以下几种,任选一种。
物体所受浮力大小可能跟液体密度有关。
物体所受浮力大小可能与物体浸入液体的深度有关。
物体所受浮力大小可能与物体重力有关。
(2)研究浮力是否与物体的形状有关。
器材:弹簧测力计、水、细线、烧杯、橡皮泥。
过程:① 用弹簧测力计测出圆柱形橡皮泥浸没水中时受的拉力 ;② 将橡皮泥捏成球形再用此法测出它浸没水中时受的拉力F2,比较F1和F2的大小即可。 ;② 将橡皮泥捏成球形再用此法测出它浸没水中时受的拉力F2,比较F1和F2的大小即可。
|
综合讲解。各个击破
【专题1】有关浮力综合题的解法初探
解与浮力有关的练习题,往往要用到力、密度、二力平衡和压强等知识,综合性比较强。学生每当遇到这样的习题,常感到束手无策,究其原因:一是所学知识不能灵活运用,相关的知识联系不到一起;二是苦思冥想,不得其法,从而失去信心。针对这些情况,结合教学实际,我总结出了突破这一难点行之有效的方法。具体步骤如下:
1.对研究对象进行受力分析。研究对象是指漂浮在液面或浸没在液体中的物体。受力分析就是找出物体在竖直方向上受到的所有力,并画出受力示意图。
2.根据力的平衡条件列方程。题目所给的研究对象大部分是静止的(即处在平衡状态)。因此,可以根据力的平衡条件列出方程。
3.解方程,求出待求的物理量。
【例1】 将一重为2牛顿的金属筒容器,开口向上放入水中时,有1/3的体积露出水面。若在筒内装入100cm3的某种液体后,金属筒有14/15的体积浸没在水中,求:
(1)金属筒的容积;(筒壁厚度忽略不计)
(2)金属筒内液体的密度。
【解析】:(1)求金属筒的容积,即金属筒的体积。
A.先对研究对象(金属筒)进行受力分析,金属筒受到有重力G和浮力F浮,受力示意图如图(2)所示。
B.由题可知,金属筒开口向上漂浮在水面上,根据力的平衡条件列方程:F浮=G

(2)求金属筒内液体的密度,仍可采用上述步骤。
A.对研究对象(金属筒)进行受力分析。金属筒受到的力有:重力G,筒内液体对筒的压力G′和水对筒的浮力F浮′,如图(3)所示。

B.由于筒静漂浮在液面上,根据力的平衡条件可列方程:G+G′=F浮′

【专题2】讨论水面是否升降的几种方法
对漂浮于水面的含杂质的冰块,熔化后是否会引起水面升降的问题,可以通过不同的途径进行分析判断。本文介绍三种简便的判断方法。
分析问题的理论依据是阿基米德原理,解决问题的途径是:对以冰块和杂质组成的系统,将冰块熔化前后系统所受的浮力的大小进行比较,或将冰块熔化成水的体积和杂质仍浸在水中体积的总和与未熔化的含杂质冰块的排水体积相比较。
一、等效法
我们可运用等效思维的方法,在保持效果不变的前提下,对研究对象、背景条件、物理过程进行重组、分解、变换、替代,使它们更简单、更符合各种理想化模型,便可达到使问题得到简化的目的。
为了增强直观性和讨论的简便,不管杂质的密度是ρ杂>ρ水或ρ杂<ρ水,我们都假定冰块和杂质是规则形体(如图1(a)示)。>
由于杂质在冰块内部与附着在冰块外部(如图1(b)示)系统排水的情况一样。为研究方便,假定杂质附着在冰块外部。
由于冰块在熔化的过程中杂质才逐渐脱离与杂质先脱离冰块才开始熔化的情况,系统最终对水面引起的效果一样。为研究的简便,假定杂质先脱离,冰块后熔化。
1.对ρ杂>ρ水的情况
杂质脱离冰块后(如图1(c)示)下沉,而冰块同时上浮,最后完全熔化成水。由于冰块上浮并熔化后系统所受的浮力减小,即系统的排水量减小,故含ρ杂>ρ水杂质的冰块熔化后会引起水面下降。
2.对ρ杂<>
脱离冰块的杂质能和冰块同时漂浮于水面(如图1(d)示),杂质脱离冰块前后,即冰块熔化前后系统在水中都是处于漂浮状态,即系统所受的浮力始终等于系统所受的重力,也就是冰块熔化前后系统所受的浮力不变,即系统的排水量不变。故含ρ杂<>
二、隔离法
设含杂质冰块的总体积为V,排水量为V排,杂质体积为V杂,冰块熔化后,化成水的体积为V化水,杂质仍浸在水中的体积为V杂浸。于是,我们可以根据以下关系进行判断。
若(V化水+V杂浸)
若(V化水+V杂浸)=V排时,冰块熔化后水面不会升降;
若(V化水+V杂浸)>V排时,冰块熔化后水面会上升。
杂质在冰块中时(如图2示)受重力G1和冰块对它的作用力F(如图3(a)示)处于平衡状态,即F=G1=ρ杂gV杂 ①
冰块受重力G2、浮力F浮和杂质对它的作用力F′(如图3(b)示)处于平衡状态,即F浮=G2+F′ ②
可将②式写为
ρ水gV排=ρ冰g(V-V杂)+ρ杂gV杂 ③
由③式可得含杂质冰块的排水量为

冰块完全熔化成水的体积为

1.对ρ杂>ρ水的情况,冰块熔化后杂质下沉,即V杂浸=V杂。
 ⑥ ⑥
∵(ρ杂-ρ冰)>(ρ水-ρ冰)
比较④、⑥式可得(V化水+V杂浸)
故含ρ杂>ρ水杂质的冰块熔化后会引起水面下降。
2.对ρ杂<ρ水的情况,冰块熔化后杂质漂浮于水面,即ρ水gv杂浸=ρ杂gv杂。>

故含ρ杂<ρ水杂质的冰块熔化后不会引起水面的升降。>
3.对含气泡的冰块,ρ气<ρ水,当气泡重忽略不计时,即可认为ρ气→0,由④、⑤、⑦式可得v气浸→0,v化水=v排,故含气泡的冰块熔化后不会引起水面的升降。>
三、极端法
我们可以运用极端思维的方法将被研究的是连续、单调变化的物理过程由一般的情况推向极端(即取物理量为极大值、极小值或临界值)进行研究,可使问题得到简化。
在ρ杂>ρ水(或ρ杂<ρ水)的情况中,不管ρ杂与ρ水相差多大,冰块熔化后对水面产生的效果始终是相同的。因此,为了研究的简便,我们可以对ρ杂取极大值或极小值进行研究。>
1.ρ杂>ρ水的情况
取ρ杂>ρ水,即可认为ρ杂很大而杂质的体积就极小。
若将杂质从冰块移出水面时,则冰块上浮,于是水面下降,冰块熔化后水面仍处于降低状态;再将杂质投入水中时,由于其体积极小,水面几乎不变动。故最终的结果仍是水面下降。
2.ρ杂<ρ水的情况>
取ρ杂<ρ水,即可认为ρ杂→0而杂质的质量极小。>
若将质量极小的杂质从冰块中移出水面时,冰块几乎不会上浮,水面也几乎不变动,冰块熔化后水面仍处于几乎不变动的状态;再将杂质投入冰中时,由于ρ杂极小,杂质质量极小,杂质几乎不浸入水中,水面几乎不变动。故最终的结果仍是水面不变动。
【例2】 如图所示,容器内分别装有水和盐水,在液面上浮着一块冰,问:(1)冰在水中熔化后,水面如何变化?(2)冰在盐水中熔化后,液面如何变化?
 
(a) (b)
图
【解析】这道题可以用计算的方法来判断,关键是比较两个体积,一是冰熔化前,排开水的体积V排,一个是冰熔化成水后,水的体积V水.求出这两个体积,再进行比较,就可得出结论.
(1)如图(a)冰在水中,熔化前处于漂浮状态.
F浮=G冰
 水g V排=m冰g 水g V排=m冰g
V排=
冰熔化成水后,质量不变:m水=m冰
求得:V水= = =
比较①和②,V水=V排
也就是冰熔化后体积变小了,恰好占据了原来冰熔化前在水中的体积.
所以,冰在水中熔化后液面不变
(2)冰在盐水中:冰熔化前处于漂浮,如图1—3—14(b),则
F盐浮=G冰
 盐水g V排盐=m冰g 盐水g V排盐=m冰g
V排盐= ① ①
冰熔化成水后,质量不变,推导与问题(1)相同.
V水= ② ②
比较①和②,因为 水= 水= 盐水 盐水
∴ V水=V排排
也就是冰熔化后占据的体积要大于原来冰熔化前在盐水中的体
所以,冰在盐水中熔化后液面上升了.
【答案】 (1)冰在水中熔化后液面不变.(2)冰在盐水中熔化后液面上升.
【专题3】设计性实验专题
设计性实验是对课本基础实验的拓展和提升,是基本知识和技能的综合运用,主要考察学生的实验技能、分析创新能力以及运用知识解决实际问题的能力。此类题的特点是:部分基本实验量具换成了其它器材,或者一些基本量具破损致使实验不能按常规方法进行,需要学生重新设计实验过程。设计思路是:认真分析题目中所缺量具和所增器材的性能和使用方法,细心组装和调整,发现和纠正实验装置或操作中的错误,对因缺少基本量具而不能直接测出来的物理量设法用其它物理概念、规律和实验方法进行合理替代,也就是找到所给器材的性能和所缺物理量间的内在联系,设计出合理简捷的实验过程并用文字、图形正确清晰地加以表达。
【例3】在探究影响浮力大小因素的活动中,同学们提出了下列三种猜想:
猜想1:浮力的大小与物 体浸入液体中的体积有关. 体浸入液体中的体积有关.
猜想2:浮力的大小与液体的密度有关.
猜想3:浮力的大小与物体的重力大小有关.
同学们通过实验探究,验证了猜想1和猜想2是正确的.
对于猜想3,甲乙两同学分别进行了如下的实验探究.
①甲同学的实验探究如下:
实验:利用弹簧测力计、水和盐水,测算出同一铁块浸没在盐水中受到的浮力大小和浸没在水中受到的浮力大小不相等.
分析:由于铁块的重力大小不变,而铁块所受的浮力大小不等,所以铁块受到的浮力大小与铁块的重力大小无关.
结论:猜想3是错误的.
②乙同学的实验探究如下:
实验:利用弹簧测力计和水,测算出体积相同的 铁块和铝块浸没在水中受到的浮力大小相等.[来源:Z.xx.k.Com] 铁块和铝块浸没在水中受到的浮力大小相等.[来源:Z.xx.k.Com]
分析:由于铁块、铝块的重力大小不等,而它们受到的浮力大小相等,所以浮力大小与重力大小无关.
结论:猜想3是错误的.
对甲乙两同学的实验,你认为 (甲同学/乙同学)的实验方法是不正确的,请具体指出他的错误是: ,根据他的实验和他的分析思路还可得出; 的结论,这个结论是 (正确/错误)的.
【解析】甲同学的实验方法是不正确的; 研究与重力的关系却控制了重力不变 ;根据他的实验和他的分析思路还可得出浮力大小与浸入液体的体积大小无关;这个结论是错误。
| 










 ⑥
⑥