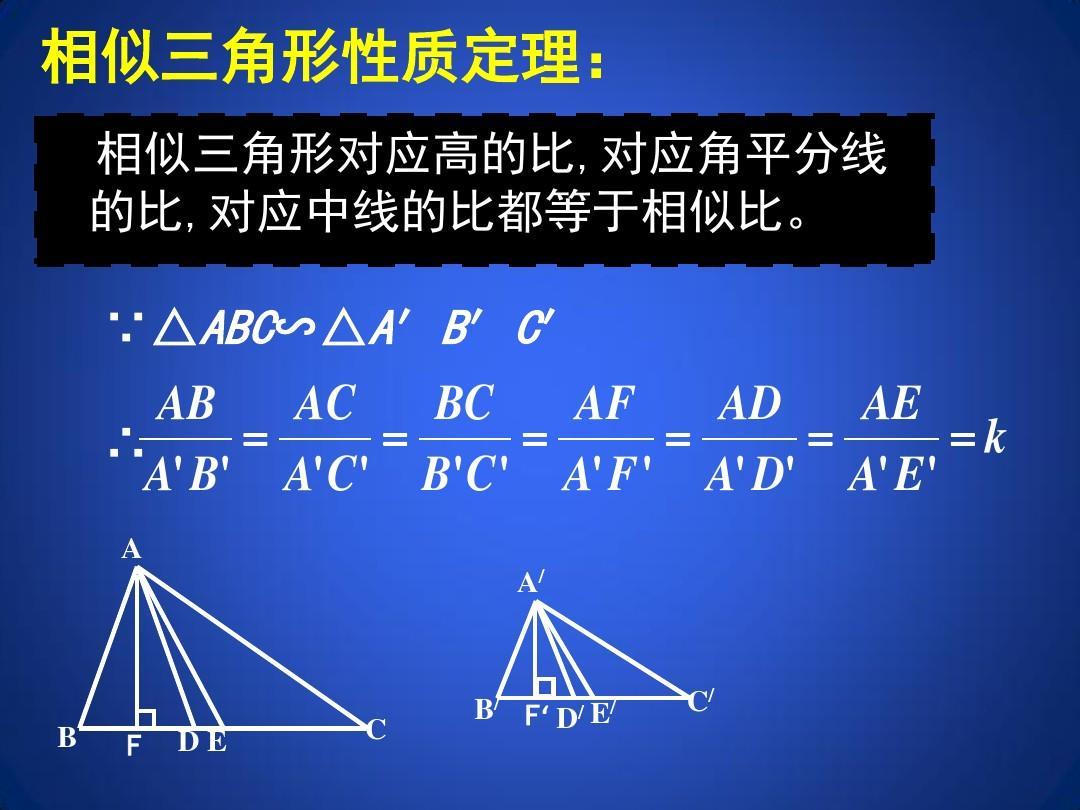
| 宜城教育365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载网www.bjtlcd.com 一、锐角三角函数的增减性
当角度在0°~90°之间变化时:
1.正弦值随着角度的增大而增大;
2.余弦值随着角度的增大而减小;
3.正切值随着角度的增大而增大。
4.锐角三角函数值都是正值.
5.正弦值随着角度的增大(或减小)而增大(或减小) ,余弦值随着角度的增大(或减小)而减小(或增大) ;
6.正切值随着角度的增大(或减小)而增大(或减小) ,余切值随着角度的增大(或减小)而减小(或增大);
7.正割值随着角度的增大(或减小)而增大(或减小),余割值随着角度的增大(或减小)而减小(或增大)。
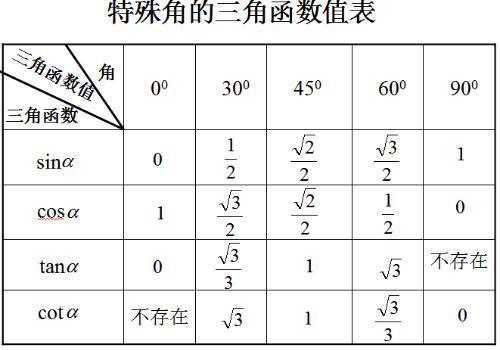
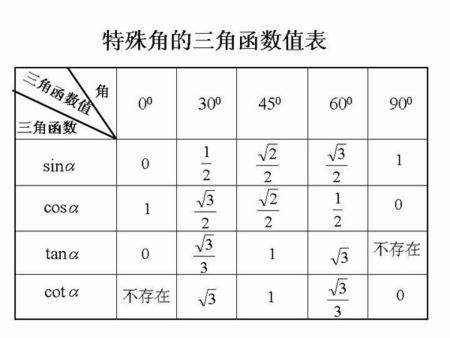
8.当角度在0°≤A≤90°间变化时,0≤sinA≤1, 1≥cosA≥0;当角度在0°0。
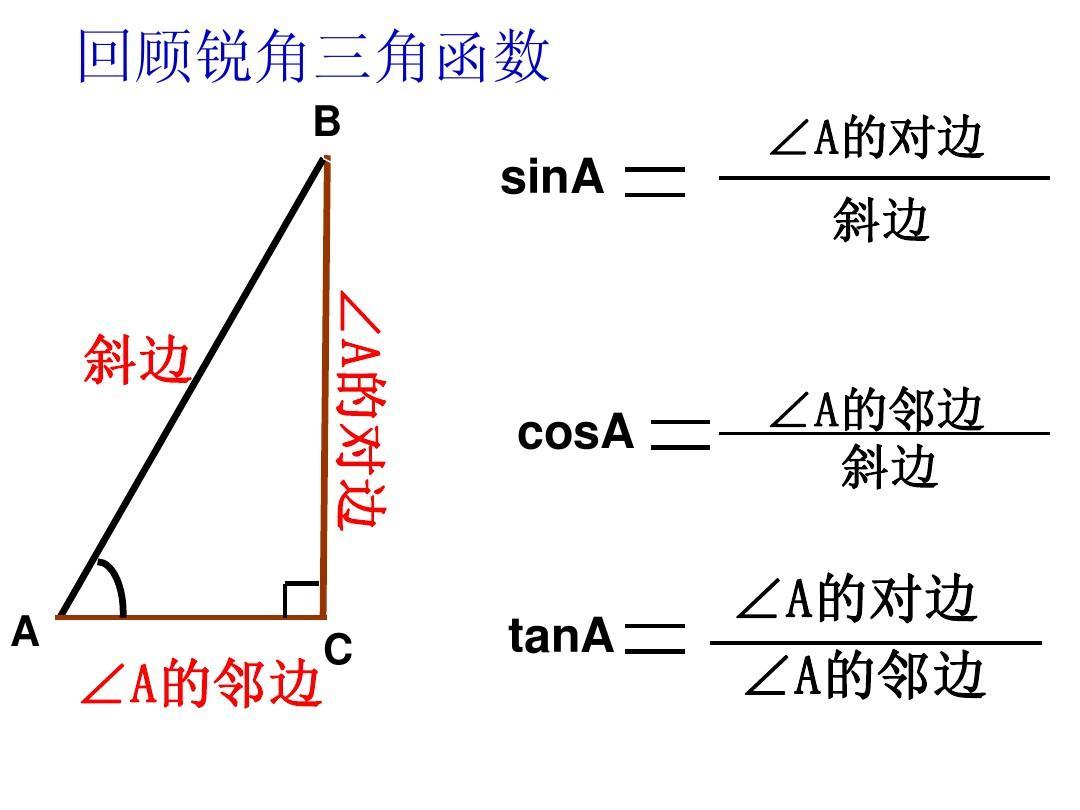
二、锐角三角函数:
锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
初中学习的 锐角三角函数值的定义方法是在直角三角形中定义的,所以在初中阶段求锐角的三角函数值,都是通过构造直角三角形来完成的,即把这个角放到某个直角三角形中。所谓锐角三角函数是指:我们初中研究的都是锐角的三角函数。初中研究的锐角的三角函数为:正弦(sin),余弦(cos),正切(tan)。
正弦:在直角三角形中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即 ;
余弦:在直角三角形中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即 ;
正切:在直角三角形中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即 ,
锐角A的正弦、余弦、正切都叫做A的锐角三角函数。
三、锐角三角函数的关系式:
同角三角函数基本关系式
tanα·cotα=1
sin2α·cos2α=1
cos2α·sin2α=1
sinα/cosα=tanα=secα/cscα
cosα/sinα=cotα=cscα/secα
(sinα)2+(cosα)2=1
1+tanα=secα
1+cotα=cscα
诱导公式
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα(其中k∈Z)
二倍角、三倍角的正弦、余弦和正切公式
Sin(2α)=2sinαcosα
Cos(2α)=(cosα)2-(sinα)2=2(cosα)2-1=1-2(sinα)2
Tan(2α)=2tanα/(1-tanα)
sin(3α)=3sinα-4sin3α=4sinα·sin(60°+α)sin(60°-α)
cos(3α)=4cos3α-3cosα=4cosα·cos(60°+α)cos(60°-α)
tan(3α)=(3tanα-tan3α)/(1-3tan2α)=tanαtan(π/3+α)tan(π/3-α)
和差化积、积化和差公式
sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]
sinαcosβ=-[sin(α+β)+sin(α-β)]
sinαsinβ=-[1][cos(α+β)-cos(α-β)]/2
cosαcosβ=[cos(α+β)+cos(α-β)]/2
sinαcosβ=[sin(α+β)+sin(α-β)]/2
cosαsinβ=[sin(α+β)-sin(α-β)]/2
宜城教育365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载网www.bjtlcd.com |