一、平行线分线段成比例定理

三条平行线截两条直线，所得对应线段成比例。
推广：过一点的一线束被平行线截得的对应线段成比例。
二、平行线分线段成比例定理推论：
①平行于三角形一边的直线截其它两边（或两边的延长线）所得对应线段成比例。
②平行于三角形一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例。
平行线分线段成比例定理：三条平行线截两条直线，所得对应线段成比例。
定理推论：平行于三角形一边的直线截其它两边（或两边的延长线）所得对应线段成比例。

 
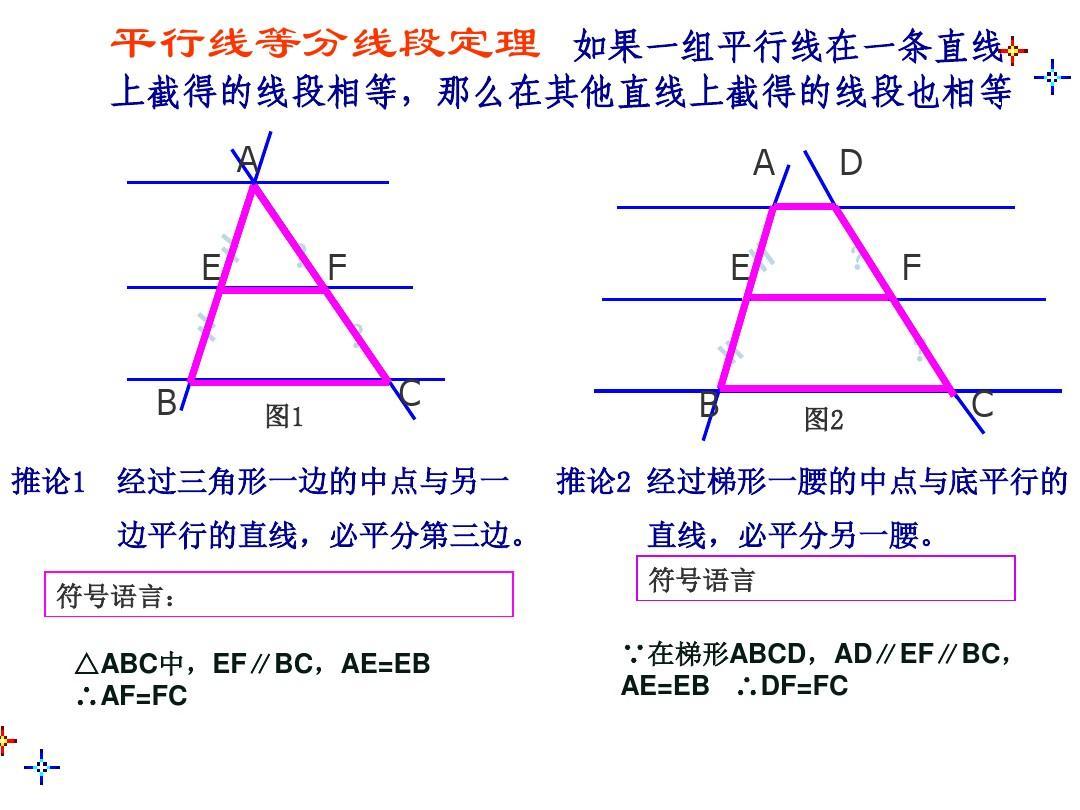
证明思路:
该定理是用举例的方法引入的，没有给出证明，严格的证明要用到我们还未学到的知识，通过举例证明，让同学们承认这个定理就可以了，重要的是要求同学们正确地使用它（用相似三角形可以证明它，在这里要用到平移和设三条平行线与直线1交于A、B、C三点，与直线2交于D、E、F三点
法1：过A作平行线的垂线交另两条平行线于M、N,过D作平行线的垂线交另两条平行线于P、Q,则四边形AMPD、ANQD均为矩形。

AM=DP，AN=DQ
AB=AM/cosA，AC=AN/cosA，∴AB/AC=AM/AN
DE=DP/cosD，DF=DQ/cosD，∴DE/DF=DP/DQ
又∵AM=DP，AN=DQ，∴AB/AC=DE/DF
根据比例的性质：
AB/(AC-AB)=DE/(DF-DE)
∴AB/BC=DE/EF
法2：过A点作AN∥DF交BE于M点，交CF于N点，则AM=DE，MN=EF.

∵ BE∥CF
∴△ABM∽△ACN.
∴AB/AC=AM/AN
∴AB/(AC-AB)=AM/(AN-AM)
∴AB/BC=DE/EF
法3：连结AE、BD、BF、CE

根据平行线的性质可得S△ABE=S△DBE， S△BCE=S△BEF
∴S△ABE/S△CBE=S△DBE/S△BFE
根据不同底等高三角形面积比等于底的比可得：
AB/BC=DE/EF
由更比性质、等比性质得：
AB/DE=BC/EF=（AB+BC)/(DE+EF）=AC/DF