一、圆心角定理

圆心角的度数等于它所对的弧的度数。
理解：(定义）
（1）等弧对等圆心角
（2）把顶点在圆心的周角等分成360份时，每一份的圆心角是1°的角．
（3）因为在同圆中相等的圆心角所对的弧相等，所以整个圆也被等分成360份，这时，把每一份这样得到的弧叫做1°的弧．
（4）圆心角的度数和它们对的弧的度数相等．
推论：
在同圆或等圆中,如果(1)两个圆心角,(2)两条弧,(3)两条弦(4)两条弦上的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等

 
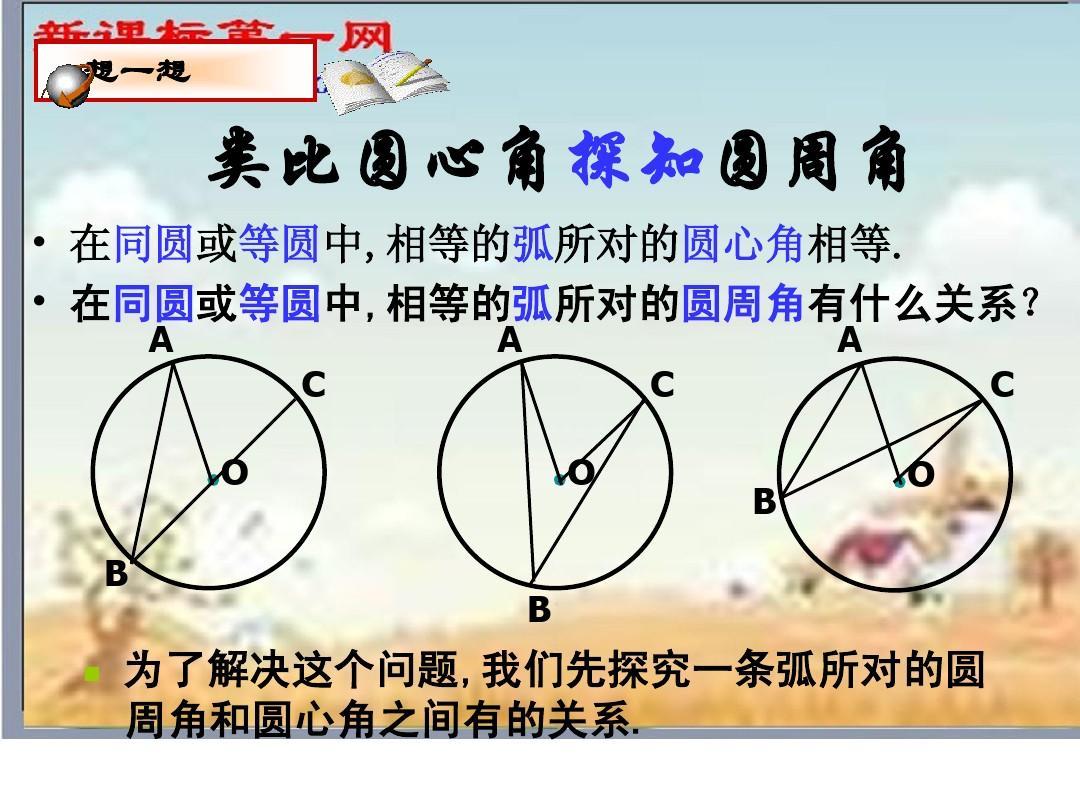
二、圆周角定理推论：
圆周角定理:在同圆或等圆中，同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。
①圆周角度数定理：圆周角的度数等于它所对的弧的度数的一半。
②同圆或等圆中，圆周角等于它所对的弧上的圆心角的一半。
③同圆或等圆中，同弧或等弧所对的圆周角相等，相等圆周角所对的弧也相等。（不在同圆或等圆中其实也相等的。注：仅限这一条。）
④半圆（或直径）所对圆周角是直角，90°的圆周角所对的弦是直径。
⑤圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。
⑥在同圆或等圆中，圆周角相等<=>弧相等<=>弦相等。
三、圆的定义:
在同一平面内，到定点的距离等于定长的点的集合叫做圆。这个定点叫做圆的圆心。图形一周的长度，就是圆的周长。
圆心角：
顶点在圆心的角叫做圆心角。
圆周角：
顶点在圆上，并且两边都和圆相交的角叫做圆周角。
圆周角的顶点在圆上，它的两边为圆的两条弦。
1、弦：连接圆上任意两点的线段。
2、弧：圆上任意两点间的部分叫做圆弧，简称弧。
弧用符号“⌒”表示以A，B为端点的弧记作“ ”，读作“圆弧AB”或“弧AB”。
优弧：大于半圆的弧（多用三个字母表示）；
劣弧：小于半圆的弧（多用两个字母表示）
圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆。
3、圆心角：顶点在圆心的角叫做圆心角。
4、弧、弦、弦心距、圆心角之间的关系定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等。
推论：在同圆或等圆中，如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。
5、圆周角：顶点在圆上，并且两边都和圆相交的角叫做圆周角。
6、圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。
推论1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等；
推论2：半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径。
四 、圆心角特征识别:
①顶点是圆心；
②两条边都与圆周相交。
计算公式:
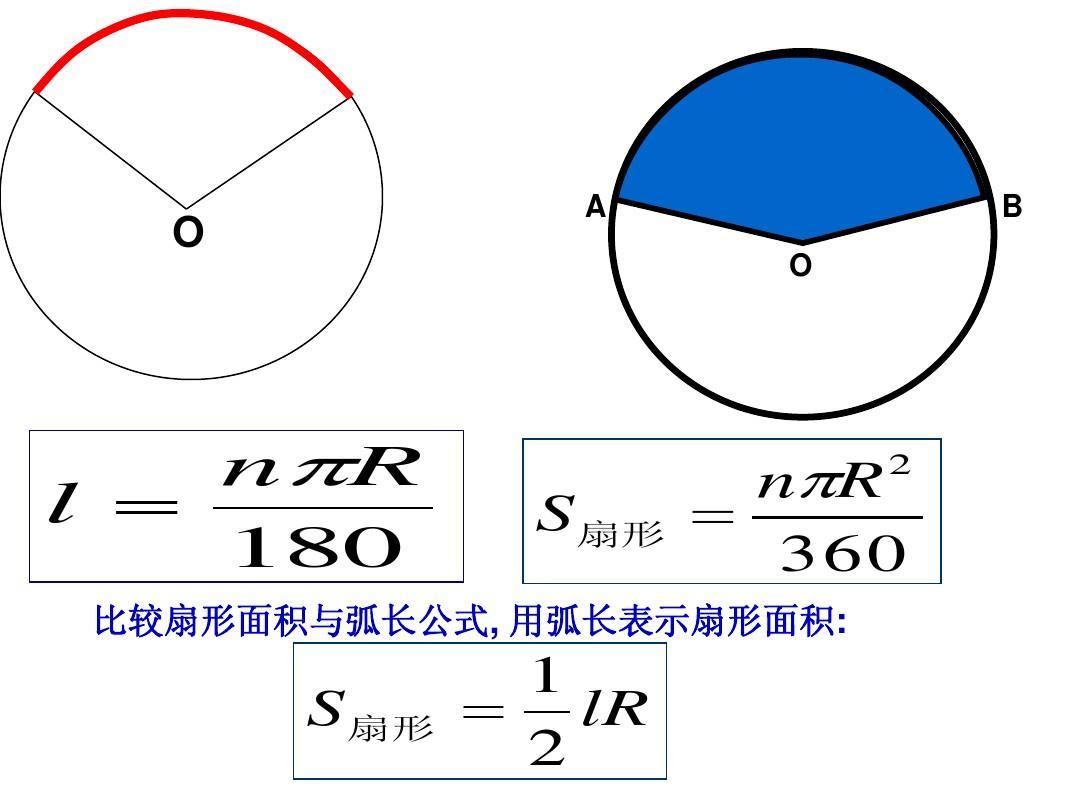
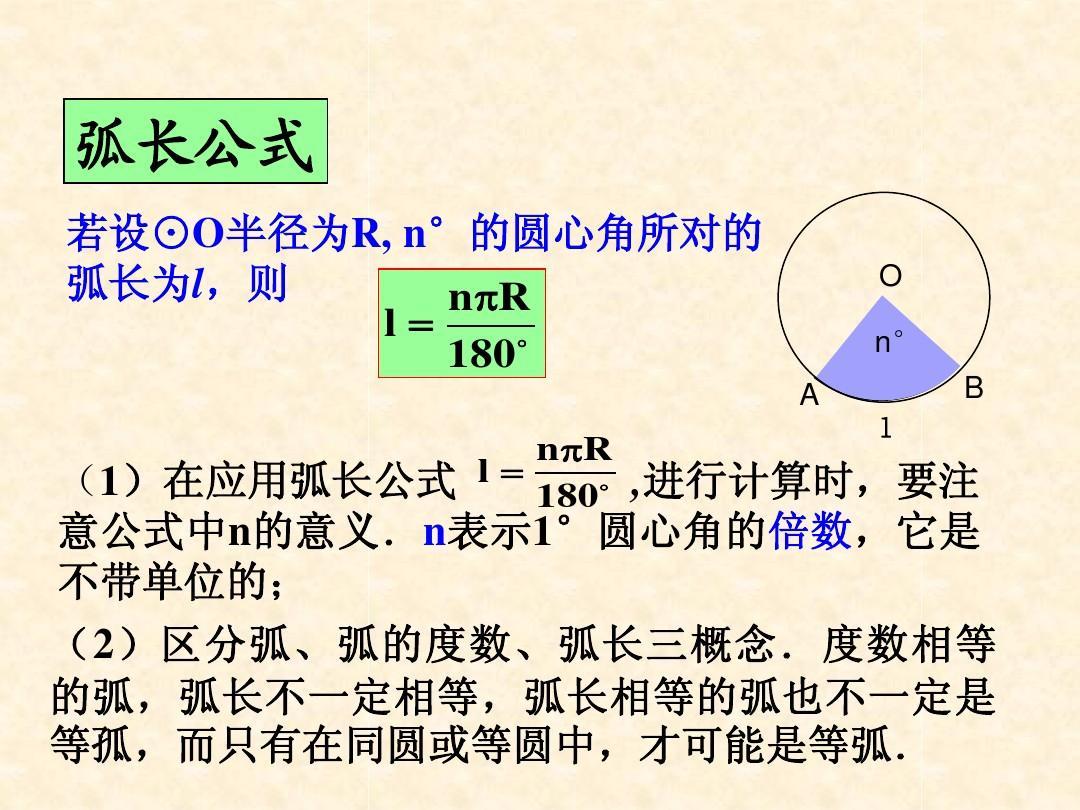
①L(弧长)=n/180Xπr（n为圆心角度数，以下同）；
②S(扇形面积) = n/360Xπr2；
③扇形圆心角n=（180L）/（πr）（度）。
④K=2Rsin(n/2) K=弦长；n=弦所对的圆心角，以度计。
与圆周角关系:
在同圆或等圆中,同弧或同弦所对的圆周角等于二分之一的圆心角。
定理证明：分三种情况讨论，始终做直径COD，利用等腰三角形等腰底角相等，外角等于两内角之和来证明。

五、圆心角定理及其推论

圆心角定理常用于数学计算，其主要功能用来计算相关圆的弧长问题。在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等。
圆心角定理推论过程：根据旋转的性质，将∠AOB绕圆心O旋转到∠A'OB'的位置时，显然∠AOB=∠A'OB'，射线OA与OA'重合，OB与OB'重合，而同圆的半径相等，OA=OA'，OB=OB'，从而点A与A'重合，B与B'重合。

因此，弧AB与弧A'B'重合，AB与A'B'重合。即弧AB=弧A'B'，AB=A'B'。则得到上面定理。
同样还可以得到：
在同圆或等圆中，如果两条弧相等，那么他们所对的圆心角相等，所对的弦相等，所对的弦心距也相等。
在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角相等，所对的弧相等，所对的弦心距也相等。
所以，在同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等。