一、三角形重心性质

1.重心到顶点的距离与重心到对边中点的距离之比为2：1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
3.重心到三角形3个顶点距离的平方和最小。
4.在平面直角坐标系中，重心的坐标是顶点坐标的算术平均，即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)；
空间直角坐标系——横坐标：(X1+X2+X3)/3纵坐标：(Y1+Y2+Y3)/3 竖坐标：（Z1+Z2+Z3）/3。
5.重心是三角形内到三边距离之积最大的点。
6.(莱布尼兹公式)三角形ABC的重心为G，点P为其内部任意一点，则
3PG2=(AP2+BP2+CP2)-1/3(AB2+BC2+CA2)。
7.在三角形ABC中，过重心G的直线交AB、AC所在直线分别于P、Q，则 AB/AP+AC/AQ=3。
8.从三角形ABC的三个顶点分别向以他们的对边为直径的圆作切线，所得的6个切点为Pi，则Pi均在以重心G为圆心，r=1/18(AB2+BC2+CA2)为半径的圆周上。
 

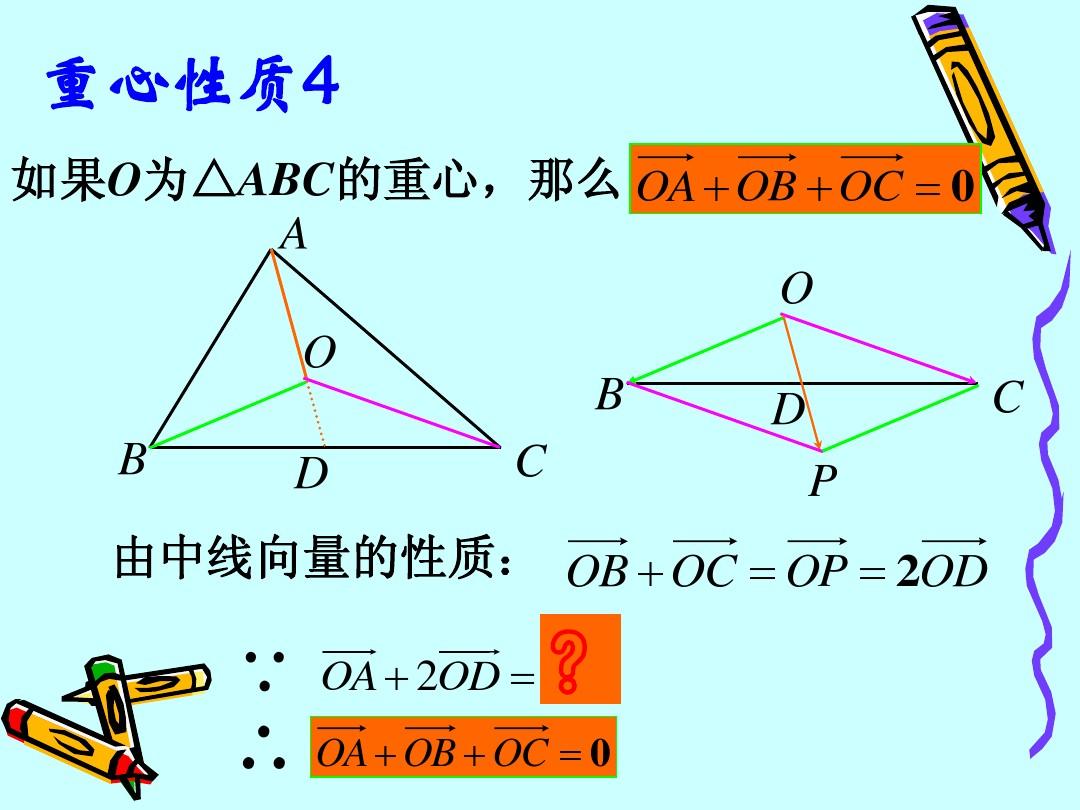
二、重心定义：
物体的重心与物体的形状有关，规则图形的重心就是它的几何中心。
如：线段，平行四边形，三角形，正多边形等等。
均匀几何体的重心：
注：下面的几何体都是均匀的，线段指细棒，平面图形指薄板。
1.三角形的重心就是三边中线的交点。线段的重心就是线段的中点。
2.平行四边形的重心就是其两条对角线的交点，也是两对对边中点连线的交点。
3.，也是六对对棱中点连线的交点，也是四对对面重心连线的交点。
4.圆的重心就是圆心，球的重心就是球心。
5.锥体的重心是顶点与底面重心连线的四等分点上最接近底面的一个。
6.四面体的重心同时也是每个定点与对面重心连线的交点，也是每条棱与对棱中点确定平面的交点。
7.正多边形的重心是其对称轴的交点。
8.由物理方法，我们可以找出任意四边形的重心。
9．物体的重心与物体的形状有关，规则图形的重心就是它的几何中心．如：线段，平行四边形，三角形，正多边形等等。
10如线段的重心是线段的中点；平行四边形的重心是对角线的交点；三角形的重心是三条中线的交点；正多边形的重心是其对称轴的交点。
由物理方法，我们可以找出任意四边形的重心。
三角形重心：
重心是三角形三边中线的交点，三线交一点可用燕尾定理证明。
三角形“五心歌”
三角形有五颗心；重、垂、内、外和旁心，
五心性质很重要，认真掌握莫记混。
重 心
三条中线定相交，交点位置真奇巧；
交点命名为“重心”，重心性质要明了；
重心分割中线段，数段之比听分晓；
长短之比二比一，灵活运用掌握好。
垂 心
三角形上作三高，三高必于垂心交；
高线分割三角形，出现直角三对整；
直角三角形有十二，构成六对相似形；
四点共圆图中有，细心分析可找清。
内 心
三角对应三顶点，角角都有平分线；
三线相交定共点，叫做“内心”有根源；
点至三边均等距，可作三角形内切圆；
此圆圆心称“内心”如此定义理当然。
外 心
三角形有六元素，三个内角有三边；
作三边的中垂线，三线相交共一点；
此点定义为“外心”，用它可作外接圆；
“内心”“外心”莫记混，“内切”“外接”是关键。