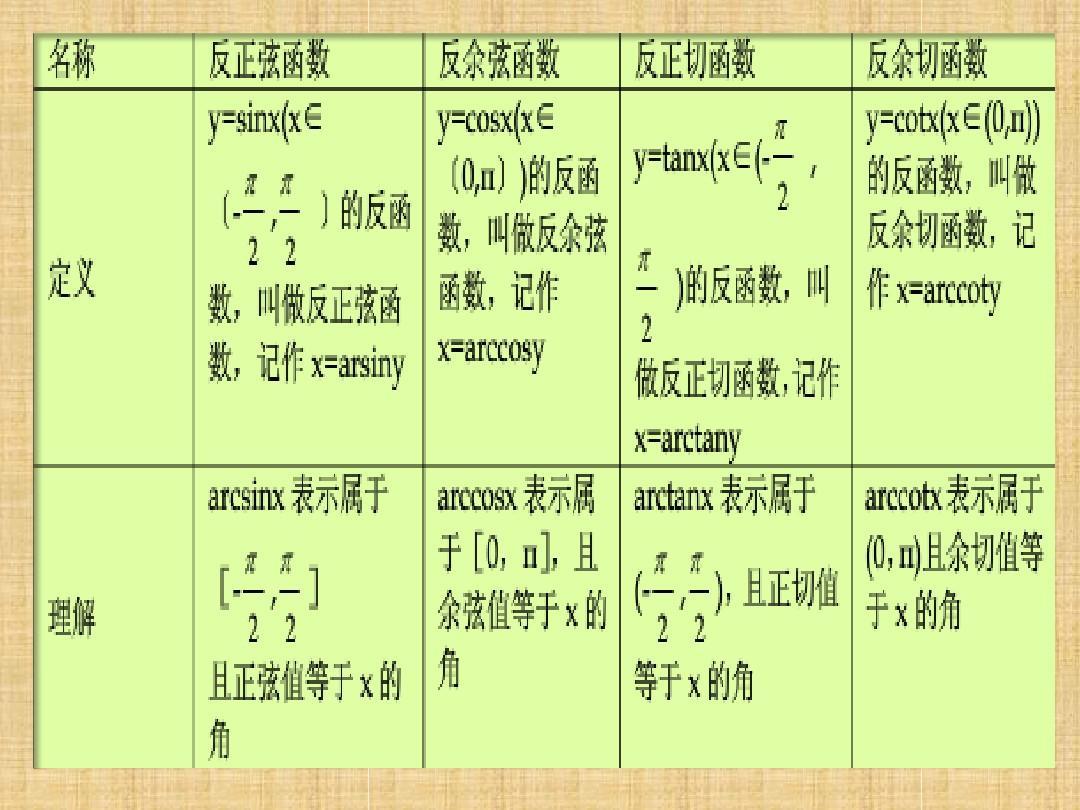
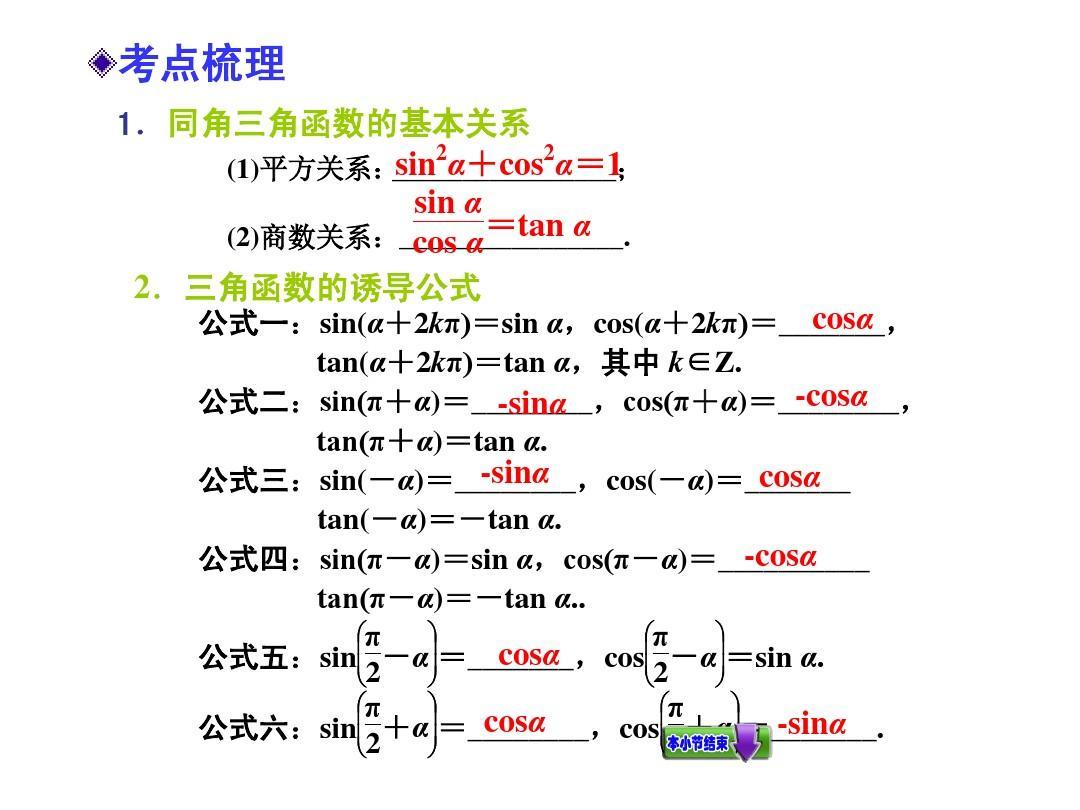
一、反函数与原函数的关系

1、反函数的定义域是原函数的值域，反函数的值域是原函数的定义域。
2、互为反函数的两个函数的图像关于直线y=x对称。
3、原函数若是奇函数，则其反函数为奇函数。
4、若函数是单调函数，则一定有反函数，且反函数的单调性与原函数的一致。
5、原函数与反函数的图像若有交点，则交点一定在直线y=x上或关于直线y=x对称出现。

二、反函数求导法则

反函数的求导法则是：反函数的导数是原函数导数的倒数。例题：求y=arcsinx的导函数。首先，函数y=arcsinx的反函数为x=siny，所以：y‘=1/sin’y=1/cosy，因为x=siny，所以cosy=√1-x2，所以y‘=1/√1-x2。
1、反函数的导数就是原函数导数的倒数。
2、设函数y=f(x)(x∈A)的值域是C，若找得到一个函数g(y)在每一处g(y)都等于x，这样的函数x=g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数，记作y=f^(-1)(x)。
反函数y=f^(-1)(x)的定义域、值域分别是函数y=f(x)的值域、定义域。
3、若一函数有反函数，此函数便称为可逆的。
4、求导是数学计算中的一个计算方法。
5、导数定义为：当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。
在一个函数存在导数时称这个函数可导或者可微分。
可导的函数一定连续。不连续的函数一定不可导。
6、除了在某几个原函数的导数为0的点以外，利用原函数的可导性就可以说明反函数可导了。