| 宜城教育365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载网www.bjtlcd.com 一、正态曲线的性质有哪些
(1)曲线在x轴上方,与x轴永不相交;
(2)曲线关于直线x=μ对称,且在x=μ两旁延伸时无限接近x轴;
(3)曲线在x=μ处达到最高点;
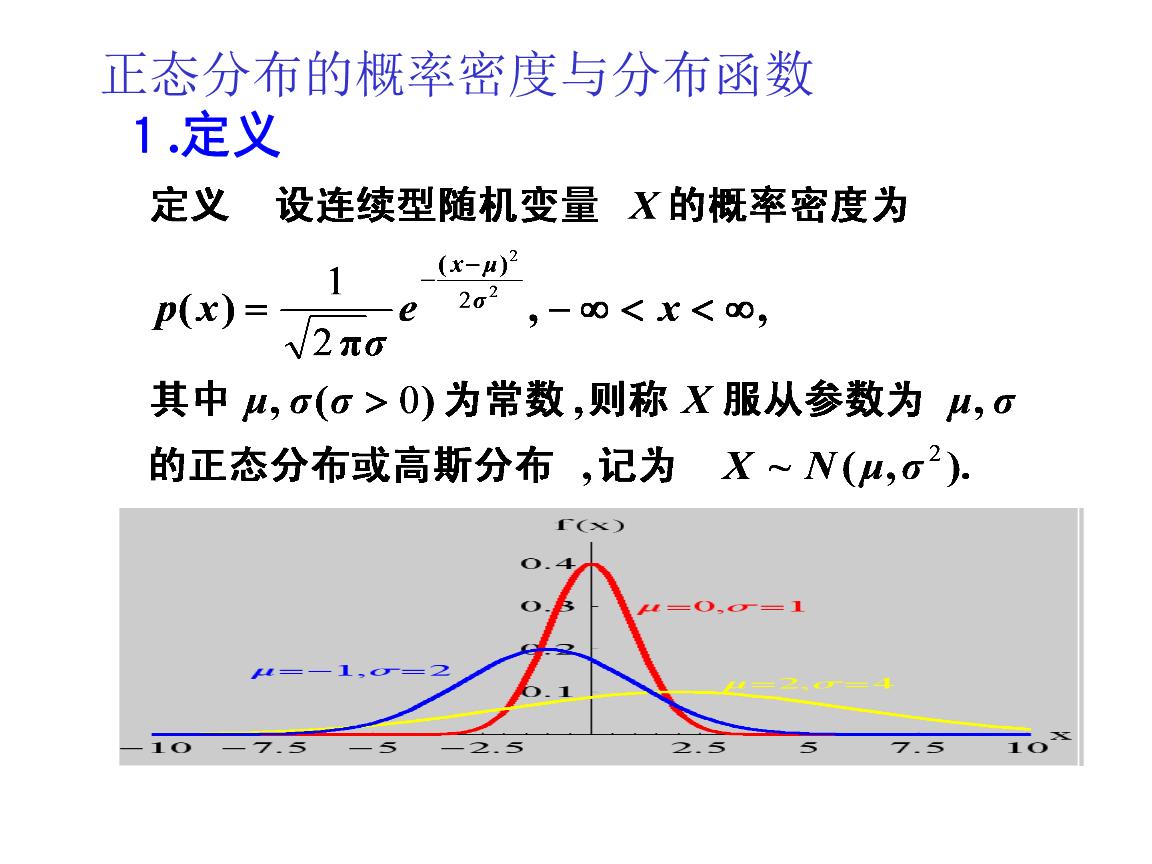
(4)当μ一定时,曲线形状由σ的大小来决定,σ越大,曲线越“矮胖”,表示总体分布比较离散,σ越小,曲线越“瘦高”,表示总体分布比较集中。
二、正态分布的定义
如果随机变量ξ的总体密度曲线是由或近似地由下面的函数给定: ,x∈R,则称ξ服从正态分布,这时的总体分布叫正态分布,其中μ表示总体平均数,σ叫标准差,正态分布常用 来表示。
当μ=0,σ=1时,称ξ服从标准正态分布,这时的总体叫标准正态总体。
叫标准正态曲线。
五、正态分布的性质
正态分布的性质:如果X1,…,Xn为独立标准常态随机变量,那么X1²+…+Xn²服从自由度为n的卡方分布。
六、正态分布相关问题
如X、Y都服从正态分布,Z=X/2+Y/3Z还服从正态分布吗?
只有相互独立的正态分布加减之后,才是正态分布。如果两个相互独立的正态分布X~N(u1,m²),Y~N(u2,n²),那么Z=X±Y仍然服从正太分布,Z~N(u1±u2,m²+n²)。
正态分布又名高斯分布,是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。若随机变量X服从一个数学期望为μ、方差为σ^2的高斯分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。因其曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是μ=0,σ=1的正态分布。
正态分布
正态分布,也称“常态分布”,又名高斯分布,最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
方差
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。
方差是衡量源数据和期望值相差的度量值。 宜城教育365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载网www.bjtlcd.com |