宜城教育365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载网www.bjtlcd.com一、二次函数最大值最小值求法
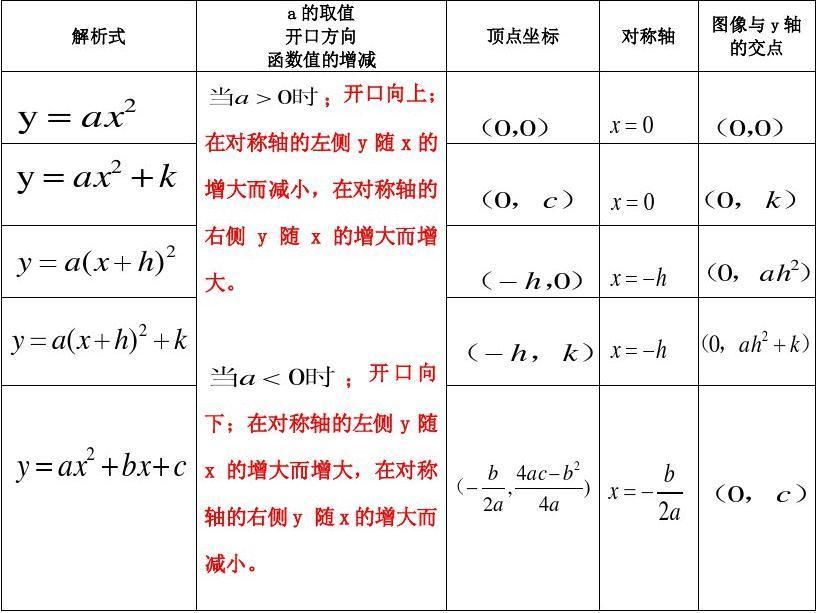
1.设函数是y=ax²+bx+c,其中a称为二次项系数,b为一次项系数,c为常数项。x为自变量,y为因变量。a>0时开口向上,有最小值,当x=-b/2a时,取得最小值为y=(4ac-b^2)/4a;a<0时开口向下,有最大值,当x=-b/2a时,取得最大值为y=(4ac-b^2)/4a。
2.二次函数的一般式是y=ax的平方+bx+c,当a大于0时开口向上,函数有最小值;当a小于0时开口向下,则函数有最大值。而顶点坐标就是(-2a分之b,4a分之4ac-b方),把a、b、c分别代入进去,求得顶点的坐标,4a分之4ac-b方就是最大值或最小值。
3.二次函数的基本表示形式为y=ax²+bx+c(a≠0)。二次函数最高次必须为二次, 二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。二次函数表达式为y=ax²+bx+c(且a≠0),它的定义是一个二次多项式(或单项式)。如果令y值等于零,则可得一个二次方程。该方程的解称为方程的根或函数的零点。
4.“变量”不同于“未知数”,不能说“二次函数是指未知数的最高次数为二次的多项式函数”。“未知数”只是一个数(具体值未知,但是只取一个值),“变量”可在一定范围内任意取值。在方程中适用“未知数”的概念(函数方程、微分方程中是未知函数,但不论是未知数还是未知函数,一般都表示一个数或函数——也会遇到特殊情况),但是函数中的字母表示的是变量,意义已经有所不同。从函数的定义也可看出二者的差别。
二、二次函数简介
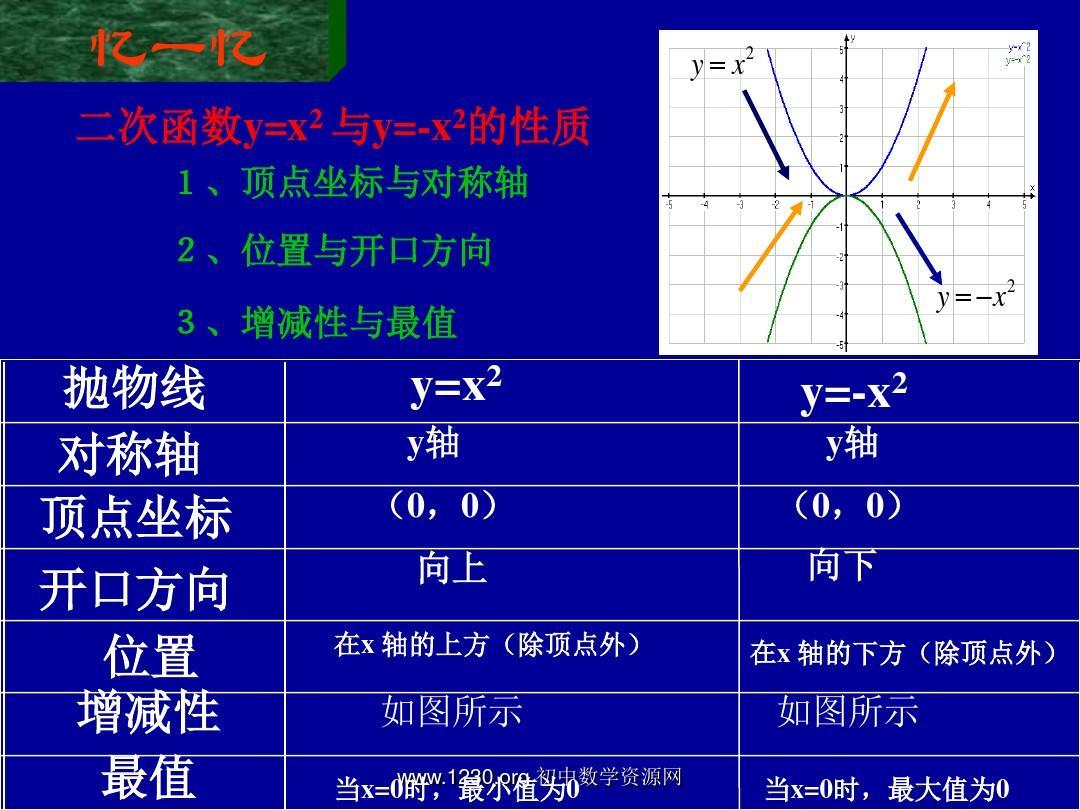
1.二次函数的基本表示形式为y=ax²+bx+c(a≠0)。二次函数最高次必须为二次,二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。
2.二次函数表达式为y=ax²+bx+c(且a≠0),它的定义是一个二次多项式(或单项式)。
3.如果令y值等于零,则可得一个二次方程。该方程的解称为方程的根或函数的零点。
4.大约在公元前480年,古巴比伦人和中国人已经使用配方法求得了二次方程的正根,但是并没有提出通用的求解方法。公元前300年左右,欧几里得提出了一种更抽象的几何方法求解二次方程。
7世纪印度的婆罗摩笈多是第一位懂得使用代数方程的人,它同时容许有正负数的根。
三、二次函数的最值:
1.如果自变量的取值范围是全体实数,则当a>0时,抛物线开口向上,有最低点,那么函数在 处取得最小值 ;
2.当a<0时,抛物线开口向下,有最高点,即当 时,函数取得最大值, 。
也即是:如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当 时, 。
3.如果自变量的取值范围是 ,那么,首先要看 是否在自变量取值范围 内,若在此范围内,则当x= 时, ;若不在此范围内,则需要考虑函数在 范围内的增减性,如果在此范围内,y随x的增大而增大,则当x=x2 时, ,当x=x1 时 ;如果在此范围内,y随x的增大而减小,则当x=x1时, ,当x=x2时 。
宜城教育365速发国际靠谱么_365bet亚洲官方网址_预付365商城下载网www.bjtlcd.com |